Last time on STAR MATH, we talked about most of the angles that explain how finding the angle of a star’s height can help us calculate how far North or South we are on the globe or, our Latitude. We’ll continue that today for the deeply curious, but first a handy Latitude flowchart for picking your method:
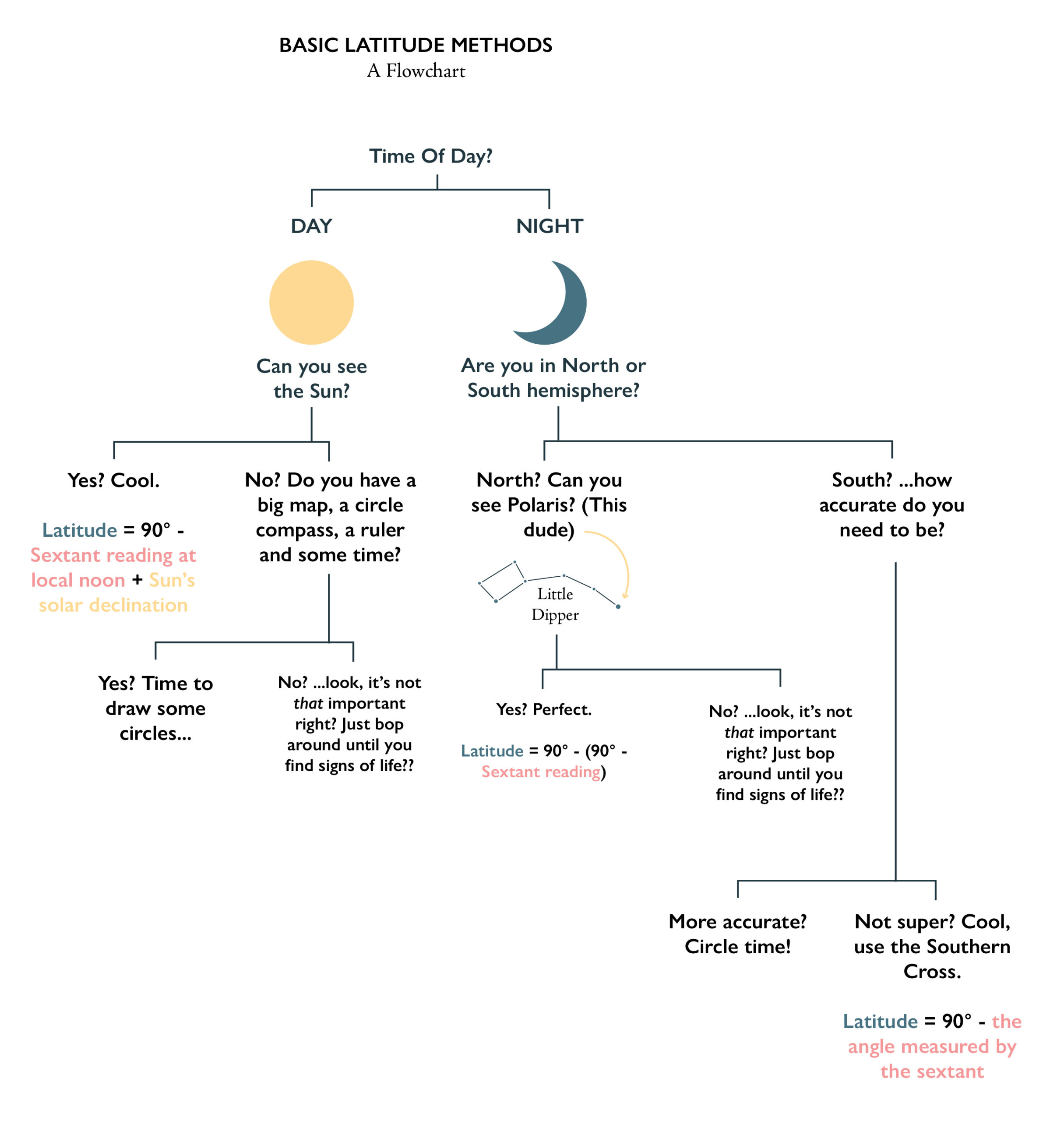
If you’re satisfied with just that information, you’re free to go! You have all the information you need to have a standard issue Grand Adventure with the basics. If you want to know Why the basics work, however, read on…
Method 1: Polaris
We’re starting with this one, because it continues our chart from before. We were just using a general star then. Now, we’re going to use Polaris. Why? It’s the only star in our sky that doesn’t seem to move. That’s because it’s house (ground point) is directly above our North Pole. If you watch the stars move, it’s like they are rotating around Polaris.
Literally, all you have to do is take a sextant reading (or sextant equivalent) of Polaris, and plug it into the formula: Latitude = 90° – (90° – the angle measured by the sextant).
If you want to know why though…
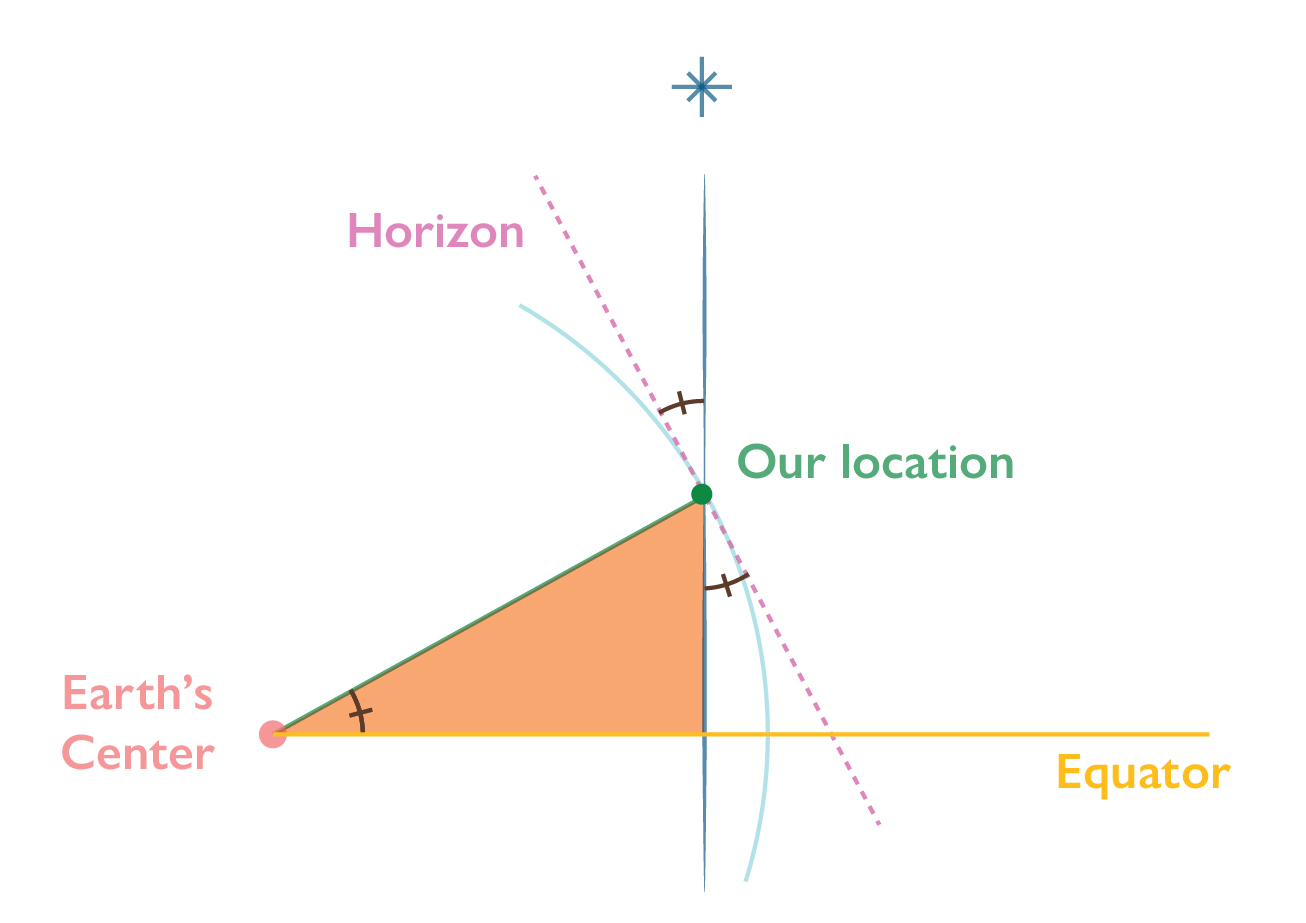
Here is our globe again. We have a line from the center of Earth to our location, the horizon line which is perpendicular to that, our line of sight to Polaris which is basically straight to the North, and our Equator.
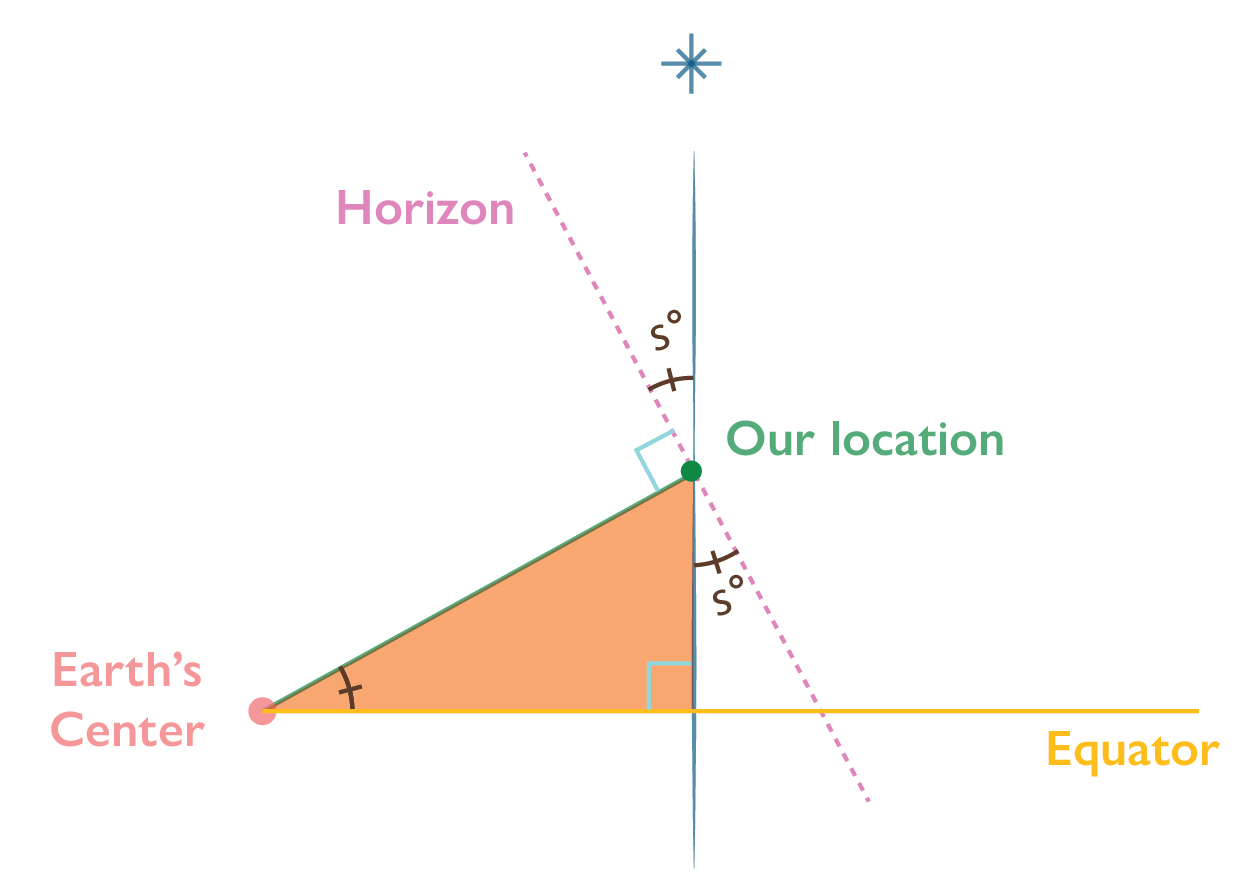
Our target is the orange triangle. Let’s fill in some angles. We can find the angle between the horizon and Polaris by using a sextant, or sextant equivalent. So that fills that in, here called s°. Remember those repeating triangles from last time? Well here are some more! We can magically fill in the same information on the other side of the line, because the angles are the same.
Remember how the horizon and our latitude line are perpendicular? That means the angle of that corner is 90° (visualized here by the blue box). But we only want a piece of that. So we just subtract the sextant reading from 90°. It’s not cheating, it’s math.
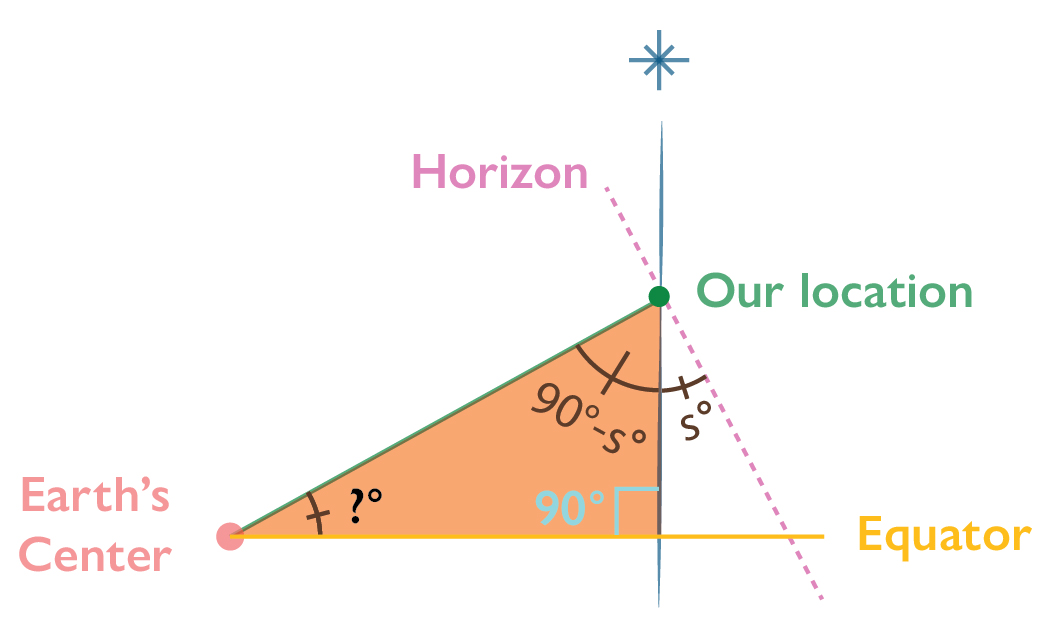
Let’s tidy that triangle up. Now we have 90°, a mystery angle that is our Latitude, and 90°- Sextant reading. Another trigonometry principle is this: All three angles of a triangle add to equal 180°. So:
180° = 90° + (90°- sextant reading) + ?
If we scramble that around:
Our Latitude = 90° – (90° – Sextant Reading)
Baboom.
Method 2 – The Southern Cross
Navigating on a clear night in the Southern Hemisphere is by far one of the coolest parts of Astronavigation. But for today’s purposes, we’re talking about actually calculating latitude. We can’t see Polaris from the South, but we can estimate where due South is, to aid in navigation, using this method.
Method 3 – Sun at Solar Noon
This one requires us to take a reading of the sun at its peak in the sky, which, if you don’t know what time zone you’re in, requires taking readings about every 15 minutes when you think it’s starting to reach the top of its arc. Even if you know what time it is, things can be muddied by Daylight Saving Time. I will not rant about that again, but… I have before.
All you have to do is take the sextant reading, and plug it into this equation:
Latitude = 90 – Sextant reading at local noon + solar declination
It’s very similar to Polaris’ reasoning, so we need not repeat all that. But what about Solar Declination?
Earth is actually cocked at an angle to the sun, rotating like a top that’s getting tired. However, the exact angle of that tilt in relation to Sun actually changes as the days progress through the year. How we calculate that is super weird:
Solar Declination = -23.44[cos((The number of days passed in the year so far + 10) * (360 / the total # of days in that year))]
Wild, right? Let’s break that into steps using the date of the day I’m writing this, 6/18/2021, a leap year:
(168 days + 10)(360/366) = 175.08
cos(175.08) = -0.98
-0.98 * -23.44 = 22.97 = Solar Declination
Stop panicking about the cosine, it’s just a button on most calculators! We have those now. Most are even solar powered.
Method 4, Plotting:
If you have some time, and like sitting with maps, you can give this method a shot. It ends up looking something like this (with a map underneath, naturally):
1 – Find a star that you can identify in the earlier part of the day. The sun works dandy. I mean, yeah, you can use the moon or Jupiter but like… You don’t have to be that hardcore.
2 – Using a sextant, or equivalent, take the angle of your chosen star’s height, and note the time.
3 – Using the date and time, look up the ground point of that star in your Nautical Almanac (because, surprise, there is a giant book that lists the exact placements of Sun, Moon, planets and several dozen stars, that we humans have calculated. Wild, isn’t it?) and plot that on your map.
4 – Sailors measure distance in Nautical Miles (Nm). Because we split Earth into angles to measure Latitude, and we know approximately how big Earth’s surface is, we know that 1° of Latitude = 60Nm.
For reasons similar to the sun method, we can use the angle of the star above the horizon, to determine the distance we are away from it. Blessedly, it is easy to convert this angle to Nautical Miles:
Nm = 60 (90° – Sextant Reading)
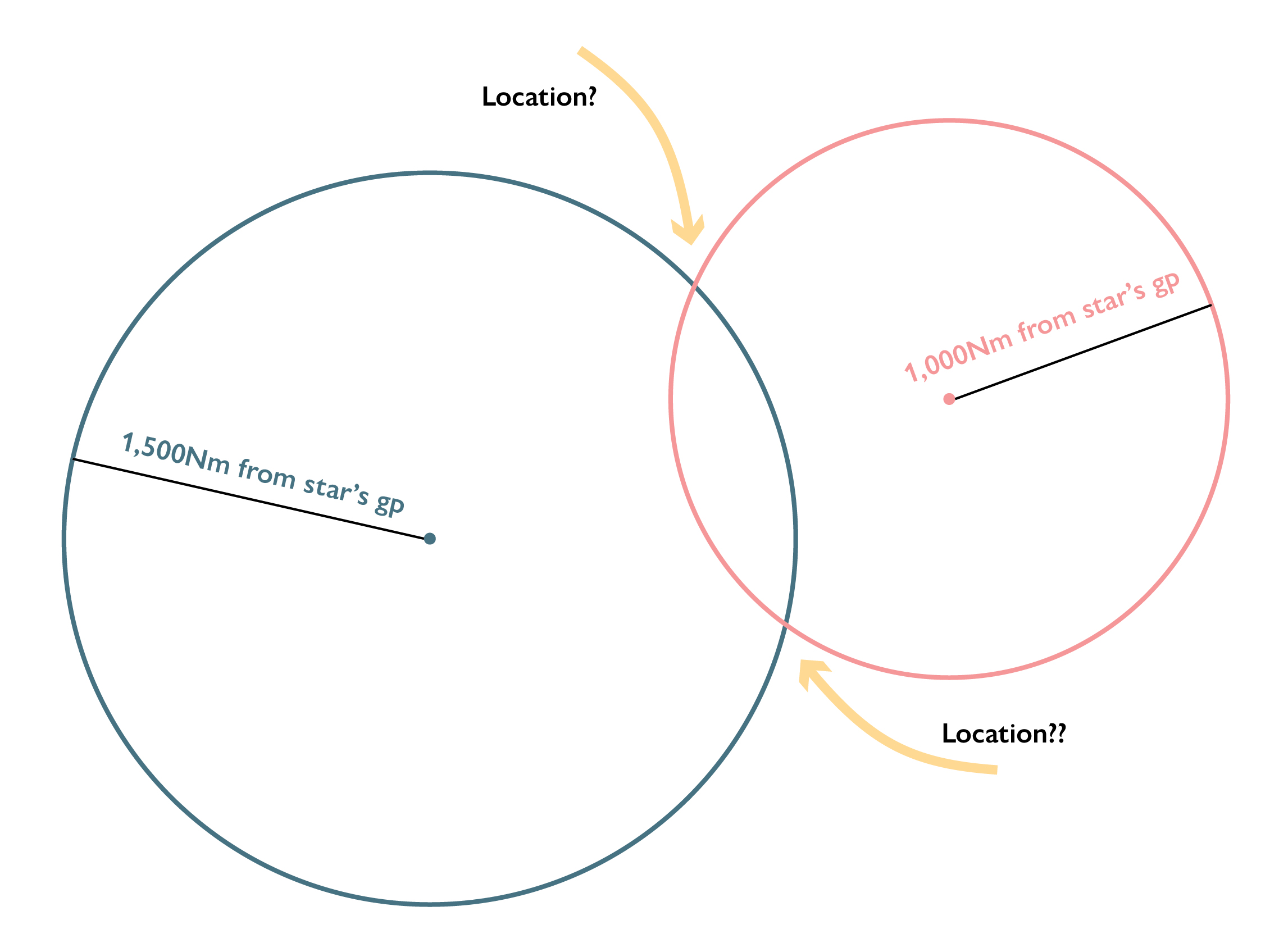
5 – Using the star’s ground point at that time, plot a circle using the distance as the radius. This is our Circle of Position. We could be anywhere along this circle. But never fear! We’ll narrow it down in a few hours.
6 – Repeat steps 1-5 in the afternoon. Now we have two overlapping circles. Where they intersect is our location. Of course, we could be in either hemisphere, but there’s a good chance you know if you’re in the Northern or Southern, due to the stars.
And that’s it! Obviously there are way more advanced methods (like a compact way to plot Line of Position, etc.), but this is the basic stuff to go out and have fun with.
Now you have a basic understanding of how to do some calculatory navigation, to better understand your location in the daytime. There’s so much more to say about celestial and natural navigation, especially at night but… that’s a story for another time!

