Star Math – Star’s House

Geometry is interesting. I personally never took a real geometry class, skipping over it and just getting the gist through other concepts. But boy did I have to do a ton of trigonometry! 

Thinking beyond math, shapes are just interesting. Life is interesting. As an artist who often has to depict a variety of real 3D objects onto a 2D plane, I’ve learned to observe life and think about how it might be rendered; broken into simple shapes. I look at how light falls on an object, and what shadow it makes. And where it’s shadow falls. 

And the direction of light is the topic of today’s post!

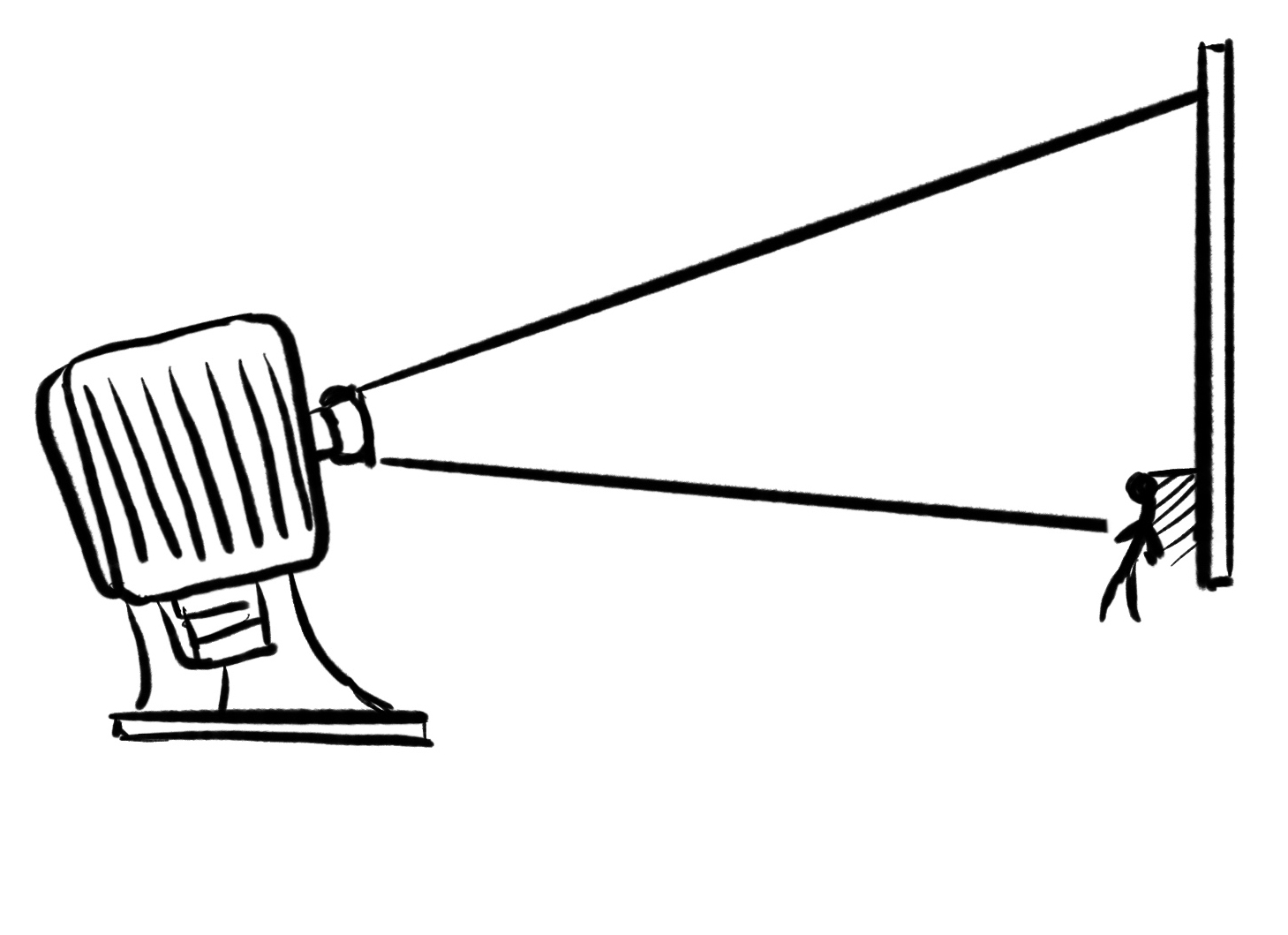
Maybe it’s just the crazy that comes from being an artist, but have you ever looked at the shape of a beam of light, in a dark room? Like a movie projector at the theater. 

The light from a movie projector is strong, and forms a cone that extends to the surface of the projection screen (or someone’s head, if they’re walking in the way).

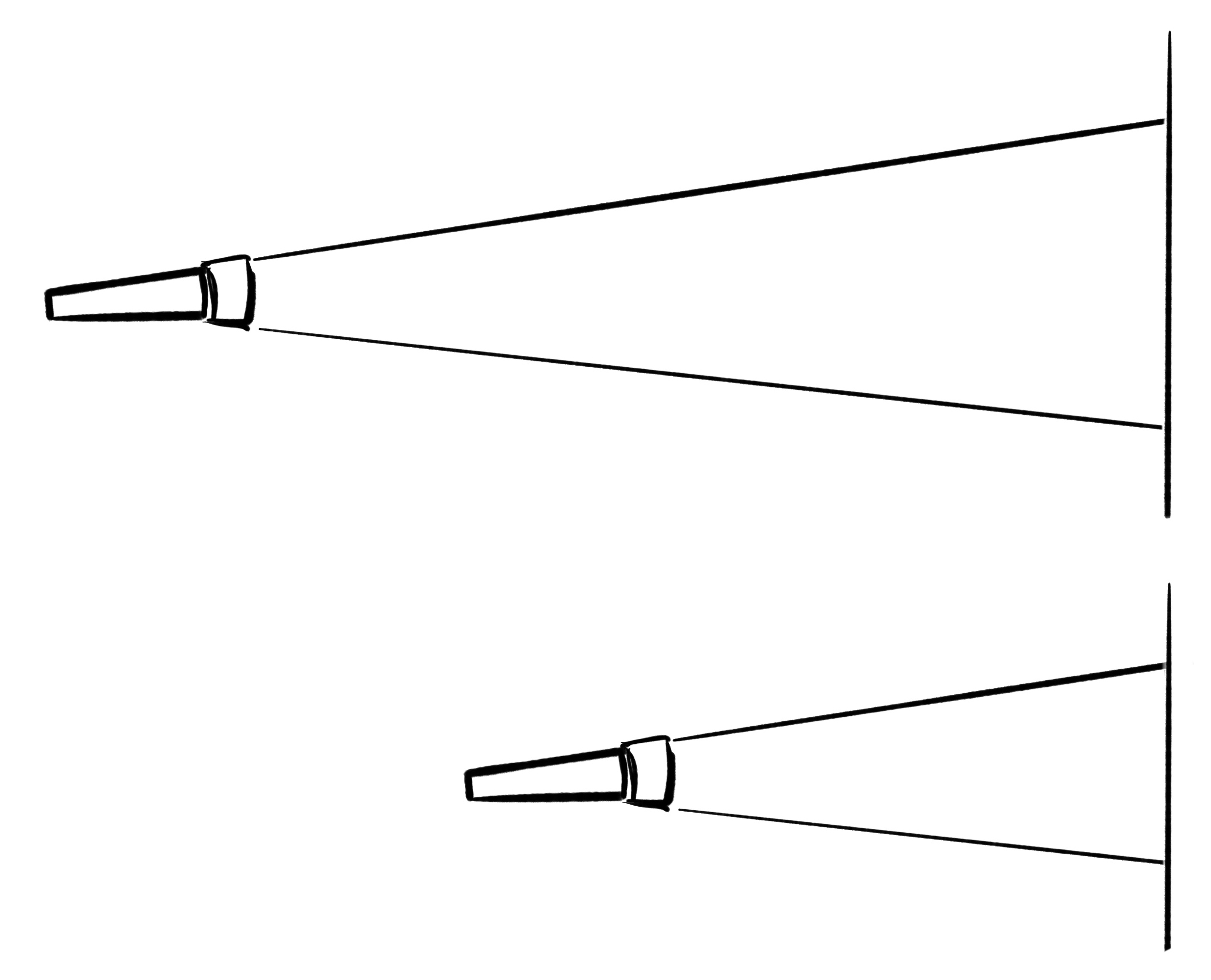
If you’ve ever made shadow puppets, you’ll see the same thing. You’ll also notice that the circle of light the flashlight makes on the wall gets smaller as you get closer, and bigger as you move the flashlight further away from the wall.

If you take a really big, strong light very far away from an object, the cone gets longer and longer… to the point that, from where you’re observing, it just looks like the beam is making a cylinder instead of a cone.

Introducing Sun:

The biggest, strongest light that Earth has!

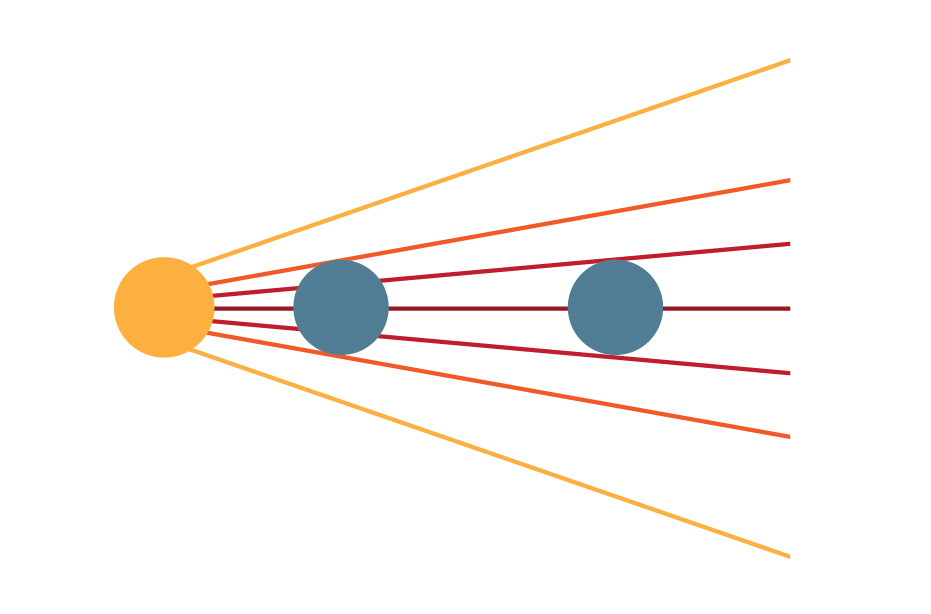
When the sun shines on Earth, its rays are essentially parallel. This goes for all stars, even though they are not strong enough to create shadows by themselves. The moon is a bit closer to us, so it has its own special set of adjustments (there’s also a few cool natural navigation tricks you can use with the moon).

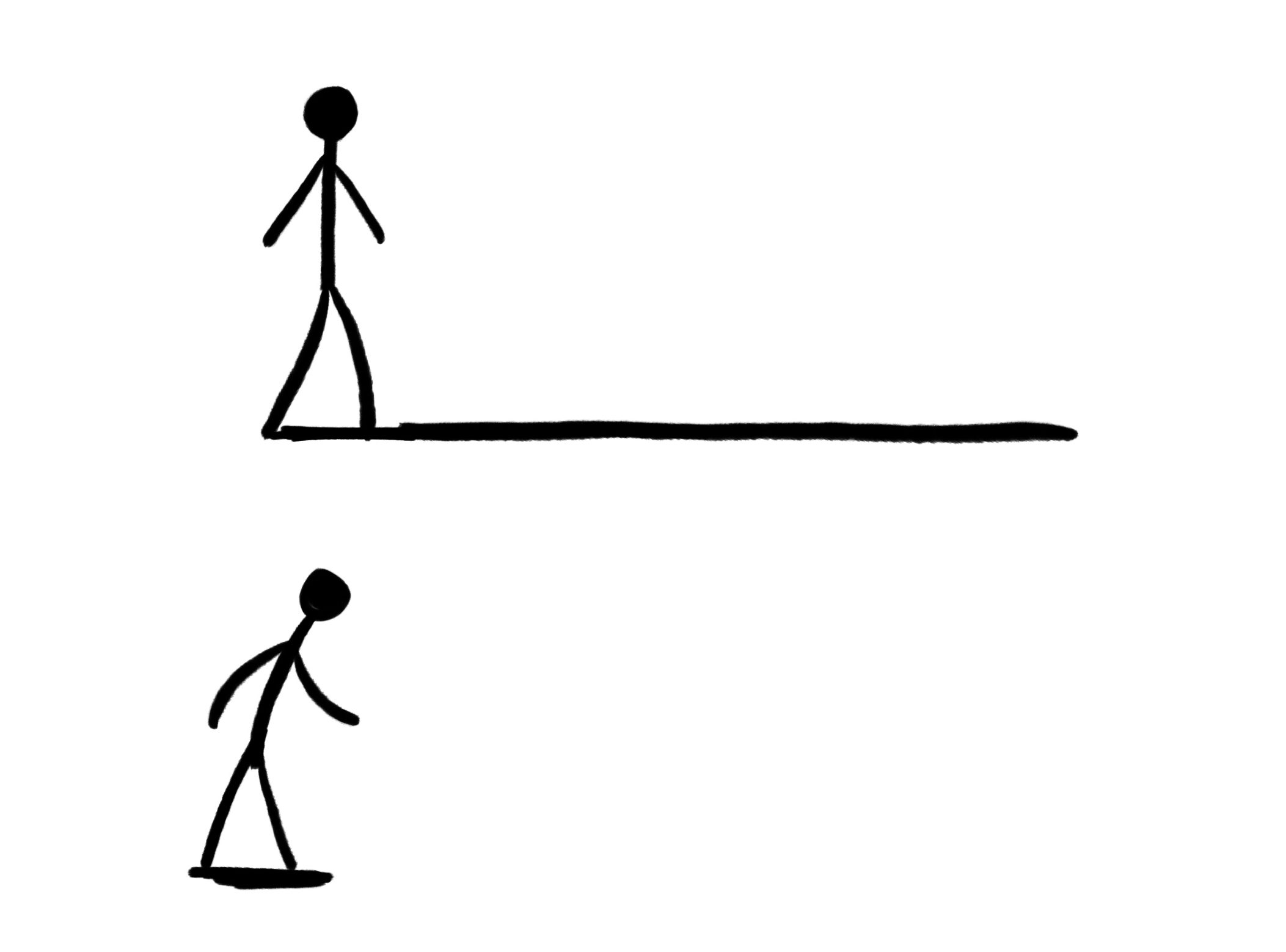
Back to shadows, have you ever noticed how long shadows stretch in the morning? As the sun rises (or sets, for that matter), shadows seem to extend for miles. Midday, however, it looks like your shadow is right under your feet!

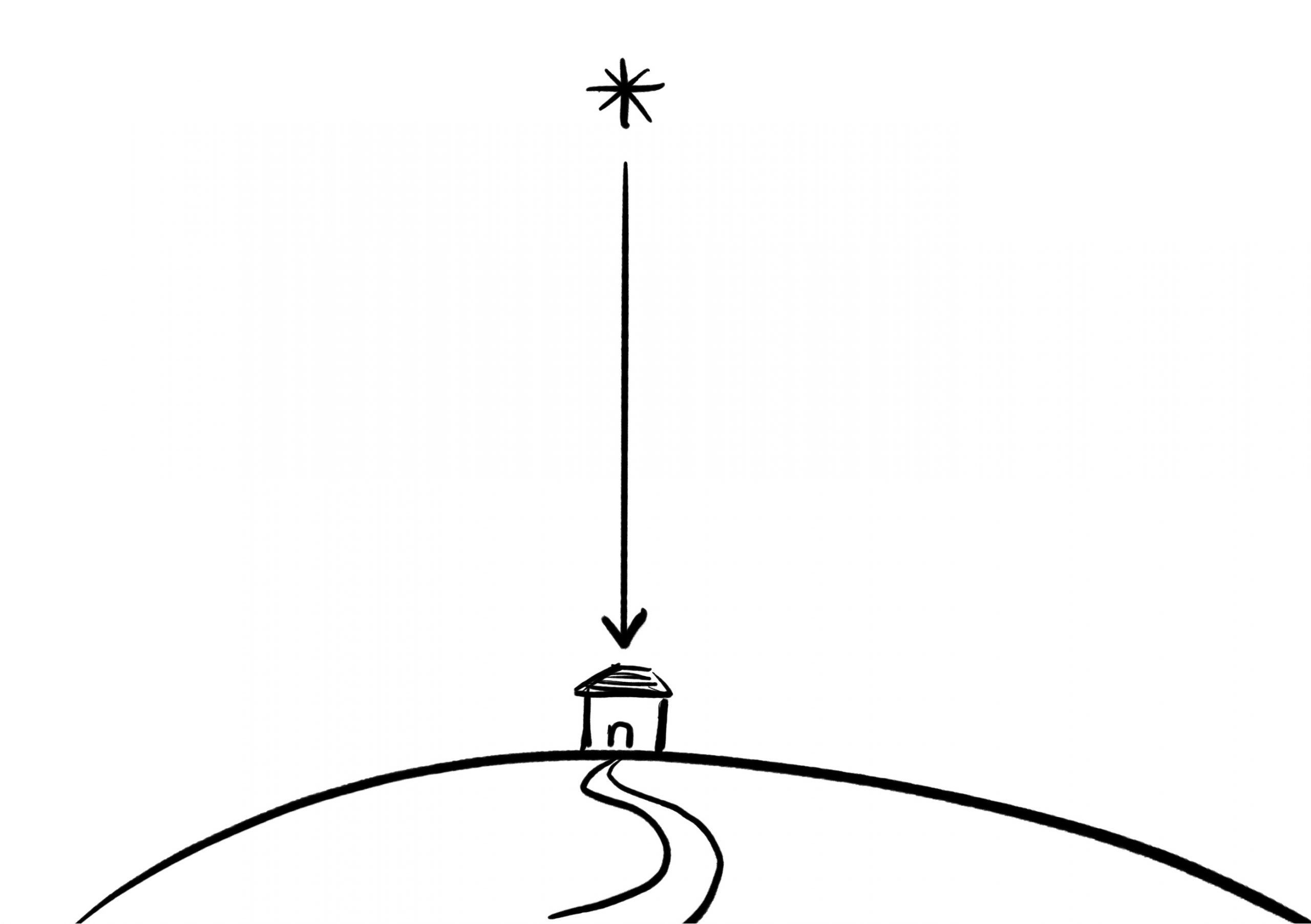
The midday sun is right over our heads, shining straight down, so we know the sun’s location at that time. The spot on Earth where the sun (or any star/heavenly body) is directly overhead, is called the celestial body’s Ground Point. Think of it as the star’s house. There is actually a book of charts (The Nautical Almanac) that contains the Ground Points of more celestial bodies than you can think of, at any time throughout the year).

Diagram Time!

So now we have a couple of concepts: Our latitude is determined by drawing a line between the center of Earth and our location on the surface (see: It’s All about the Angles); stars have houses–Their Ground Point indicates their exact location at a given time; and the light from heavenly bodies shines down to earth in parallel rays.

Let’s start putting all that together!

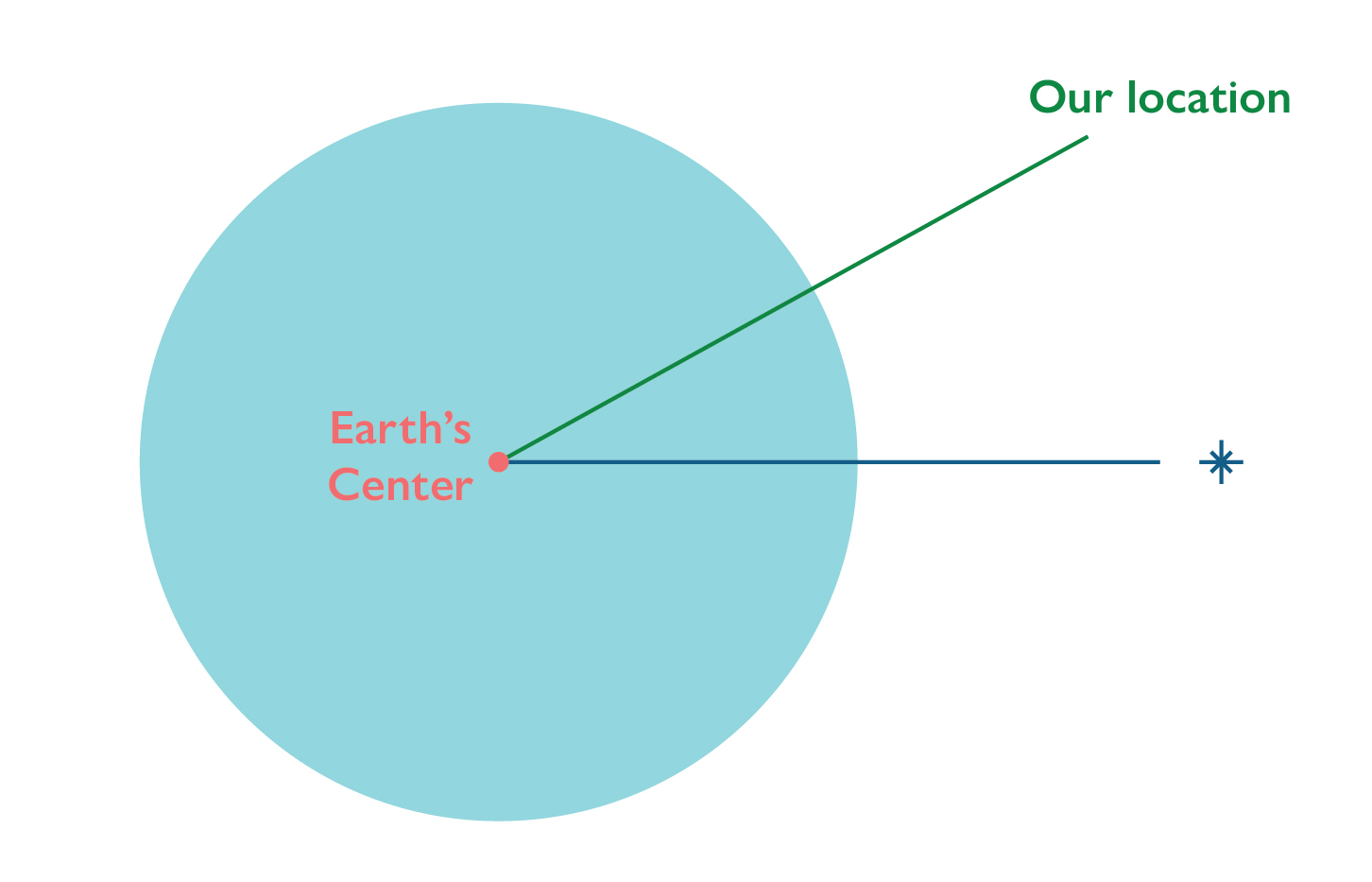
Here’s Earth with its center, a line extending from it through our location on the surface of the planet, and the star we can see from where we are, a line drawn down through it’s ground point on the surface of Earth. 

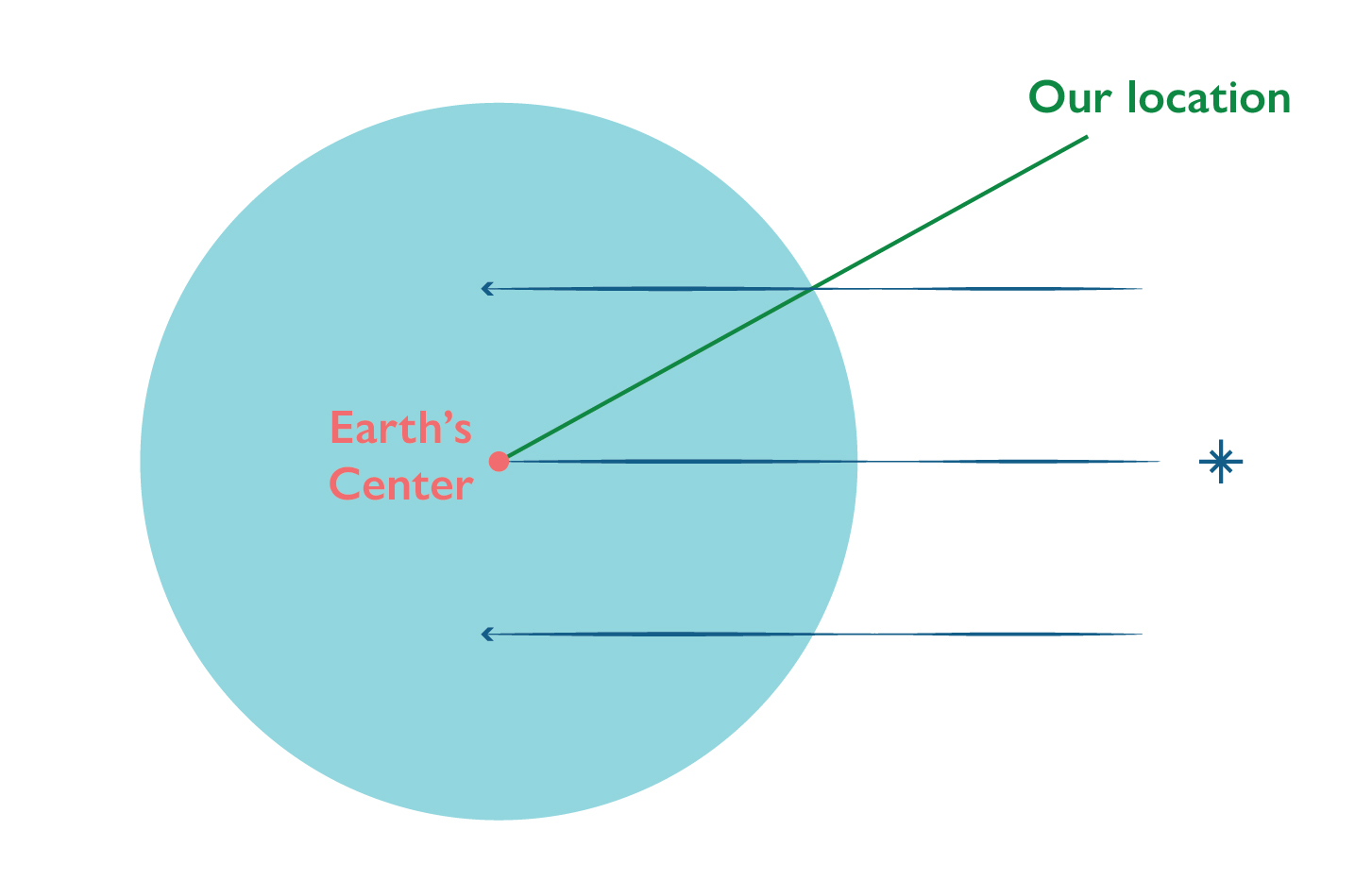
Here’s the light shining down from the star, all parallel (ish, honestly the difference is so small that it doesn’t affect calculations at all).

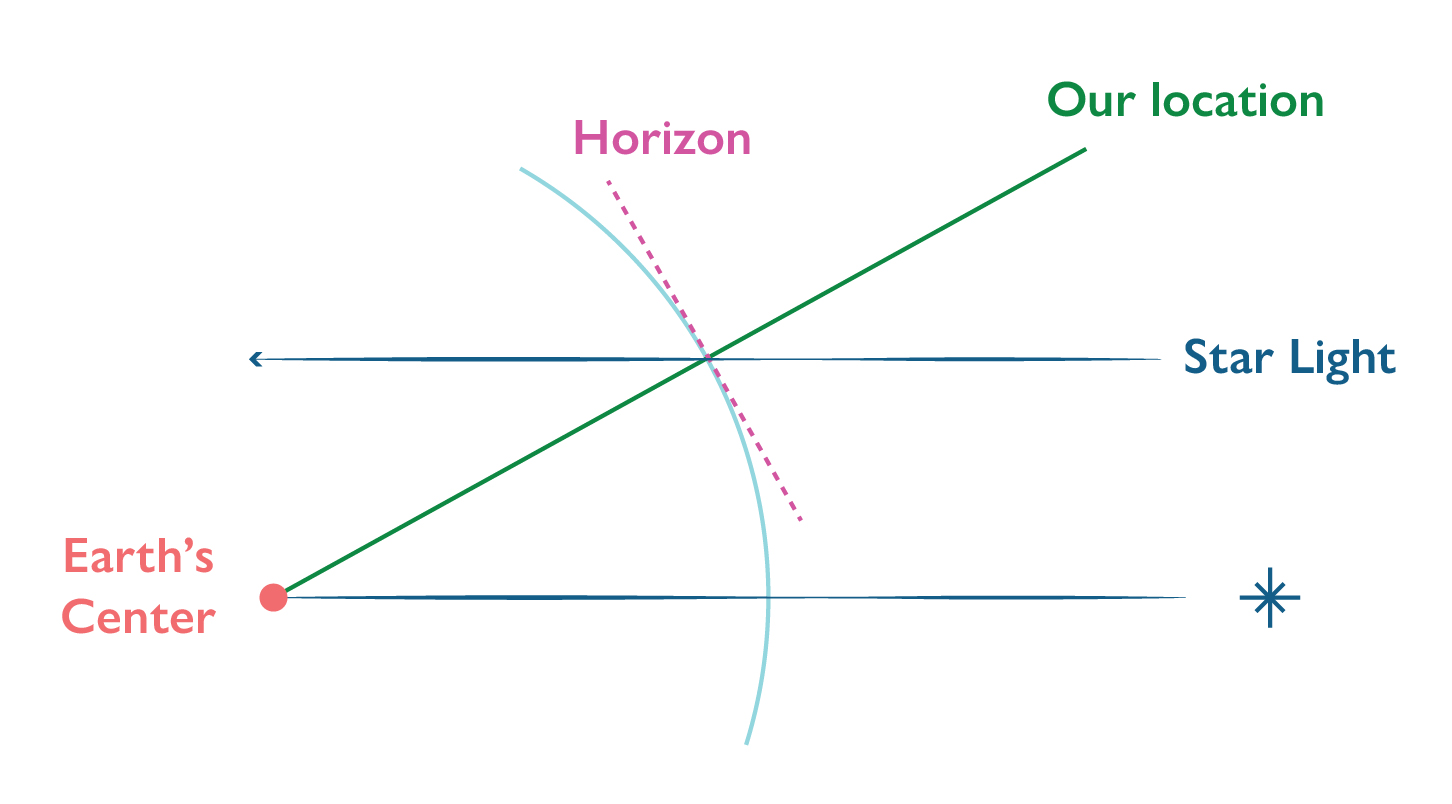
Let’s zoom into that surface. We’re going to add the Horizon line. It is parallel to the line of our location.

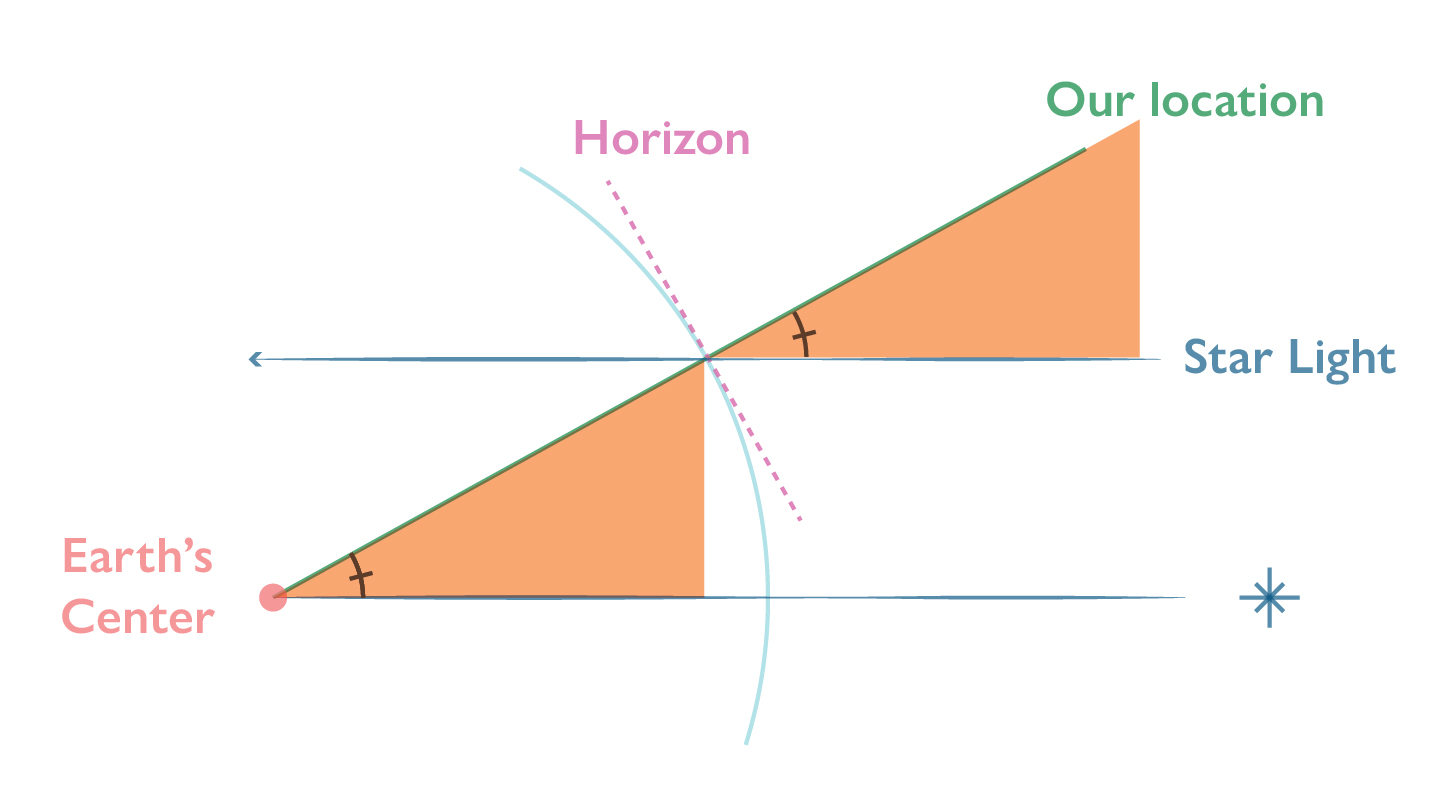
So we have all this stuff. It’s really a lot of stuff! I’ll chat about how we use this to calculate our latitude next time, so for now, let’s end on some observation: notice how the triangle (colored orange) that is formed by the center of Earth, our location line and the star’s ground point line, is the same as the other triangle that is formed by our location line and the parallel beam of light (also orange)?

Here’s where some trigonometry knowledge comes in: They are the same triangle, because they were formed using the same angles!

We will be finding out what those angles are, therefore finding our latitude, next time on… STAR MATH!