This page is dedicated to my ongoing research on the physics of a Minotaur getting stuck in a wall. That’s the kind of silliness we get up to here!

Here’s the sequence we’ll be discussing on this page:
First up, we want to determine how hard the Minotaur will impact the wall (or Mirin, for that matter).
We are assuming that:
- Common Bull Speed = 25 mi/hr
- Common Bull Weight = 2,200 lbs OR 1,000 kg
First, I’m going to get the velocity of the bull by switching miles per hour into meters per second:

Now we use a collision equation in order to calculate the impact:
Kinetic Energy = 0.5 x mass x velocity2
KEMinotaur = 0.5 (1,000 kg)(11.17 m/s)2 = 62,451.48 J
For comparison, let’s take a look at a car. Most of the time, a car is going between 25-35 miles per hour, and is slightly heavier than a Minotaur, so:
KECar = 0.5 (1,200 kg)(15 m/s)2 = 135,000 J
So the impact of a Minotaur is about half that of a car going normal street speeds, but it’s honestly going to pack a wallop; especially the horns.
Speaking of the horns, let’s tackle that next.
Assuming the horns would not shatter upon impact, and did indeed get stuck in the wall, how much pulling force would it take to overcome the force of static friction holding them in place, and free the Minotaur?
Take a look at this box on a hill:
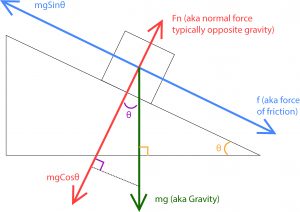
We’re looking for f, the force of friction. Using our trigonometry skills, we can see that the force of friction is exactly opposite the expression mgSinθ.
For this calculation, we’re going to half the bull’s weight to compensate for the help of his hind legs, and we’re going to assume that Mirin has dipped his head about 20 degrees downward, so he is stuck at an angle, much like our diagram. Therefore:
f = mgSinθ
f = (1,000 kg /2)(9.8 m/s) x Sin(20) = 1675.89 N
Now, I don’t personally know how much force a bull can pull with, especially not backward and with the torso of a man with a limp… BUT we do know that a bull can pull about 2,000 kg (about twice its weight), so there’s a good chance that he’d be able to get himself out, providing that the pressure of the surrounding wall did not keep creating an issue.
Stay tuned! I will update this page with further figuring as we hammer out more equations! The “how far would the horns stick in the wall” bit has given us some headaches!

Woolmancy is the YA tale of a best-friend break up, set in a world of magical weavers and lightning sheep.


