Conditions have not been great for conducting a survey, heat smoke, and now the local peoples are carrying out some sort of construction project.
But it’s been a great time to get some practice in, sighting horizontal distances! There’s some math involved, but it’s actually very simple and requires only one formula.
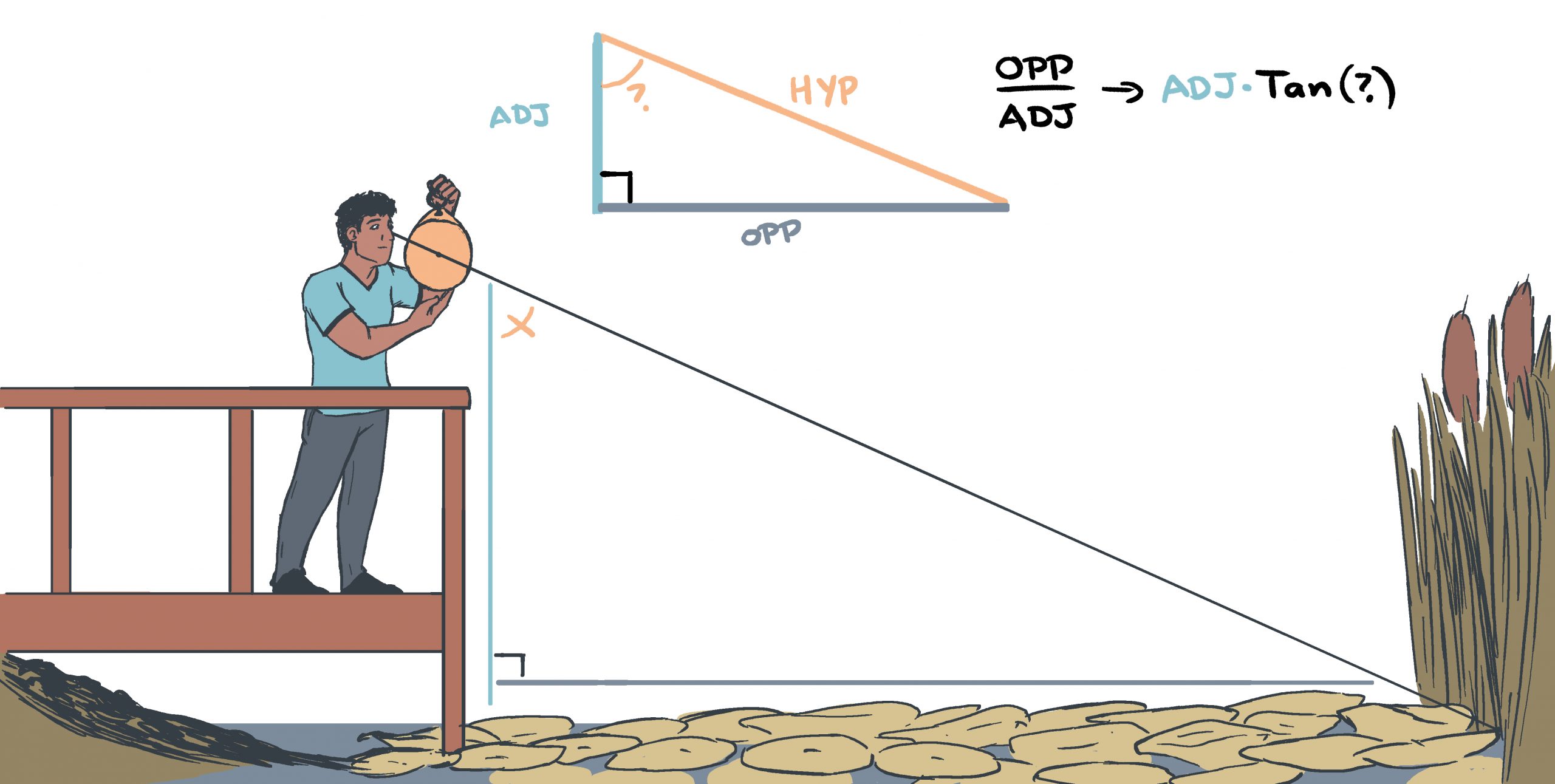
Using an astrolabe (with or without the shadow square pictured below), I just need to know how far above the waterline I am (my height up to my eyeline + the dock or boat deck height), and the angle from my eye, to the coastline. Then a quick plug into the calculator and we have our distance! This is also how celestial navigation works too, but with vertical angles. But that’s a story for an upcoming post!
An Example
Let’s say the dock is 2ft above the water, and the distance from my feet to my eyes is 5ft. So that tall (adjacent to the angle) side, is 7ft tall.
Then I look through my astrolabe, adjust the arms to line up, and it says that the angle is 60°.
So we just use the tangent formula. I could explain why, but it looks like this: 7ft x tan(60°)
Our answer is that the shore is 12.12ft away from us!
Medieval Trigonometry
But what about medieval sailors that didn’t have calculators?
Okay, real talk, since there was no great way to pinpoint longitude, they didn’t really know where they were anyway. So knowing that a feature was 300 meters away from a ship that has no definable position has is not terribly helpful for a mapmaker (unless they’re triangulating to figure out the length of the shore, but that’s another talk too). An experienced sailor can estimate distance by eye from the horizon, using a similar technique, so there was not the need to calculate exact positioning, though it could be done.
But even on land, how was it done by your average cartographer? Trigonometry tables!
 Trigonometry Tables
Trigonometry Tables
By the middle ages, brilliant mathematicians had been working with angle math for literal centuries. After all, star angles is where all of our navigation, including GPS, comes from.
The scan to the left is not a trigonometry table, specifically, but there were all sorts of tables available then, as well as now (we’ll get back to that when we swing round to celestial navigation). So if I needed to know the tangent of 60°, I could look it up in a table, then multiply it by my measured height. Easy! Or at least easier than trying to do it all by hand, right?
Above: Original work by Muhammad al-Qunawi (died 1524) – Scan: King, David A. (1977). “Astronomical Timekeeping in Ottoman Turkey”. International Symposium On the Observatories in Islam: p. 258. Original: Topkapi Palace T 1618: Ahmed III 3499
Next Mapping Steps
As for our map, as soon as I’m able, I will head over and measure the lake of grass, the meadow, and the thickness of the trail (which may resolve some of the areas that don’t meet up as well. Then I will toss in some artistic rendering and our map will be complete! It will be nice to finally have explored this wild wilderness fully.
